Derivative : solution exercise 1 (Intermediate math level)
Given the quadratic equation y = 3x2 + 2 and the function y = (1/2)x3 - 1, you are asked to :
a) Calculate the derivative y ' of both functions
-
y ' = (3x2 + 2) ' = 6x
y ' = (0,5x3 - 1) ' = 1,5x2 = (3/2)x2
b) Compute, for both curves, the slope of their tangent lines at x = 1
using the derivatives figured out hereabove
The slope of the tangent line to a curve at x = 1 is the value of its derivative at x = 1.
y ' = f '(x) = 6x
f '(1) = 6 . 1 = 6 = slope of the tangent line to the curve y = 3x2 + 2 at x = 1-
y ' = f '(x) = (3/2)x2
f '(1) = (3/2) . 12 = 3/2 = slope of the tangent line to the curve y = (1/2)x3 - 1
at x = 1
c) Find the equation of both tangent lines
-
For y = 3x2 + 2, its tangent line at x = 1 is the tangent line to the curve at the point
x = 1 and y = 3 . 12 + 2 = 5, thus I know that my tangent line passes through the point (1 ; 5). I also know that the tangent line has a slope of a = 6. Let us now compute the equation of this tangent line :
General cartesian equation of a straight line : y = ax + b
Equation of the tangent line : y = 6x + b ...
... that passes through the point (1 ; 5) : 5 = 6 . 1 + b
thus 5 - 6 = b
Which yields b = -1
Conclusion : the tangent line to the curve y = 3x2 + 2 at x = 1 is y = 6x - 1
-
We use the same method to figure out the equation of the tangent line to the curve
y = (1/2)x3 - 1 at x = 1
The tangent line passes through the point that has an x-coordinate = 1
and an y-coordinate = 0,5 . 13 - 1 = -0,5 = -1/2
Equation of the tangent line that has a slope a = 3/2 through the point (1 ; -1/2) :
y = (3/2)x + b
-1/2 = (3/2) . 1 + b
Thus -(1/2) - (3/2) = b
Which yields b = -4/2 = -2
Conclusion : the tangent line to the curve y = (1/2)x3 - 1 at x = 1 is
y = (3/2)x - 2
d) Trace both curves and its tangent lines on a graph
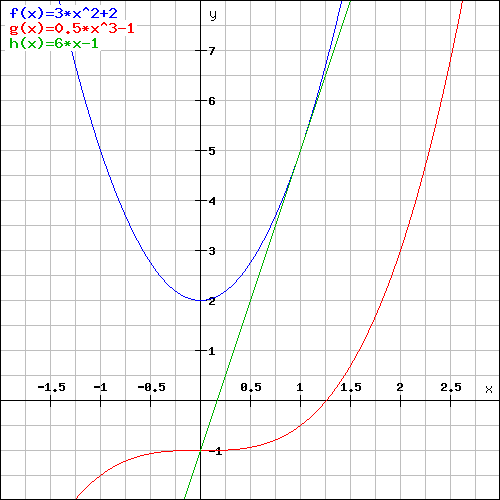
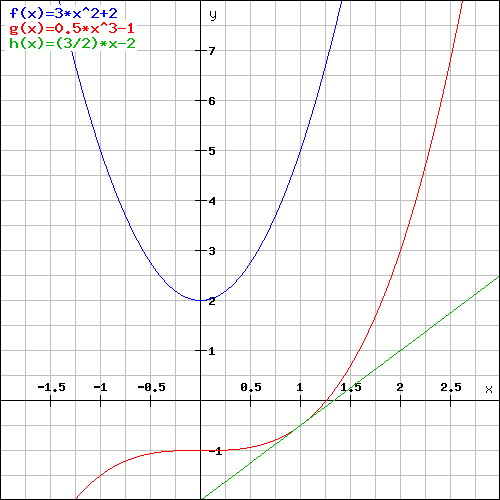
Both graphs have been drawn with our free online Graph Plotter which is a real scientific graphing calculator that enables you to trace any mathematical function online.