Advanced Math Level lesson with derivative exercises and answers online
This applied math course in biology, medicine, physics and economics will teach you, for instance, how to use derivatives theory to maximize your profit in economics.
This is an advanced placement calculus lesson, terefore before you start the following math exercises, we advice you to make sure you are able to solve easily the basic math level exercises and the intermediate math level exercises.
Advanced Math Level: useful to whom ?
to those of you who truly want to understand the use of the derivatives thanks to practical exercises applied to biology, medicine, economy, industry,...
to the students who want to start studying sciences and who want to make sure they have a good math level before the beginning of the course at university or college,
to the senior high school students who want to prepare a math exam or a math test for their AP Calculus class (Advanced Placement Calculus) or to prepare the SAT, ACT or another math test,
-
to the students who are in their freshman year in college or at the university,
Derivative exercises : Content
2. Very difficult and mean derivatives
4. Derivatives applied to biology, medicine and economy
4.5 The diameter of your trachea is reduced by 33% of its original diameter when you are coughing
4.6 Cost and revenue in economics : maximize your profit (marginal cost, marginal revenue)
1. Optimization
1.1 Two numbers are hiding themselves Solution 1.1
Two numbers are hiding themselves, however we do know that those two numbers have a sum equal to 12. Find those two numbers :
a) such that the sum of their squares is minimum,
b) such that the product of one number and the square of the other number is maximum,
c) such that the product of one number and the cube of the other number is maximum,
1.2 The biggest steel container Solution 1.2
There is a surge in steel price. Indeed steel prices have almost doubled in the past year : the price of steel was 400 euros per ton in 2007 and rose to reach 700 euros per tonne in 2008 (1 metric tone = 1000 kg). It is therefore critical to save as much steel as possible in order to ensure business profitability. Hence you have to design the largest container with the smallest surface area possible and minimise material waste during cutting steel sheets.
You are asked to find the dimensions of the largest open top container that you could possibly manufacture using a rectangular steel sheet of 24 m2 (sheet area = 24 square meters). To do so you must cut equals squares from the 4 corners of the steel sheet and then fold up the sides. One of the sides of the sheet has to measure 6 m.
1.3 A farmer wants to set up a fence around his field Solution 1.3
A farmer whishes to build a fence around his rectangular field and to divide it in two equal parts as well. The dividing fence must be parallel to one of the side of the field. You are asked to find the dimensions of the field of maximum area that you can fence and divide in two equal parts with a wire fence of 1200 m.
1.4 Harvest your rice at the right time to maximize your profit Solution 1.4
As you know, export rice price is on the rise : export rice prices have doubled between february 2007 and february 2008 to reach near historical levels with 40 eurocents/kg. Thus creating serious food problems in the many poor regions of the world. If a farmer harvests his rice today, he will get 1200 kg of rice for a market price of 40 eurocents/kg. However, if the farmer decides to wait to sell his rice, his harvest will gain 100 kg per week, wich is great! But the rice market price is falling and for each week he is waiting, the price is reduced by 2 eurocents/kg. When should our farmer harvest his rice to maximise his profit (maximum profit)?
1.5 Henry Ford and its moving assembly line Solution 1.5
In a factory where cars are being manufactured on an Assembly Line, the car is assembled thanks to the genius of the American founder of the Ford Motor Company (Henry Ford was openly sympathetic to the Nazis and Anti-Semite,... well, a bad guy. Nevertheless he invented and created the first moving assembly line in 1906). However, before the car is assembled, the doors of the car must be painted. Therefore a huge steel cylindrical tank contains 64 m3 of paint (when it is full). You are asked to find the dimensions of that cylindrical tank in order to minimize the quantity of steel required to make it. The point is to save raw material and thus Earth's limited resources. Important note: the cylindrical tank is closed at both ends by a lid.
2. Very difficult and mean derivatives
Calculate the derivative of the following functions and simplify your answer as much as possible.
2.1 
Solution 2.1
2.2 .GIF "how calculate the derivative of a function")
.GIF "derivative rules")
2.3 .GIF "Mathematics and chain rule")
.GIF)
2.4 .GIF "If you compute the slope of a line segments which get closer and closer to the point itself, and eventually taking the limit of this process, you will get the derivative of the function at that point")
.GIF "The derivative of a function at a given point is the slope of the curve at that point")
3. Derivative and graph
3.1 Derivative and slope calculation
Given the following graph :
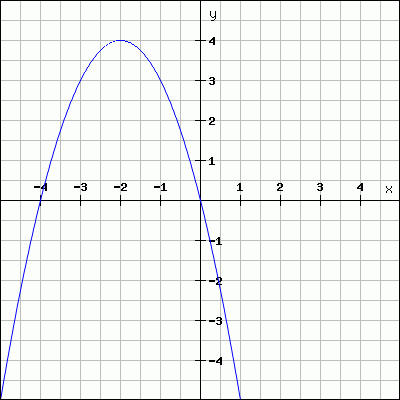
You are asked to :
a) Estimate the slope of the curve at x = -2 and at x = -4 using the formula slope =
, thus calculating the slope of the tangent line to the curve.
b) Given the equation of the parabola shown hereabove: y = -(x + 2)2 + 4, calculate the value of its derivative at x = -2 and at x = -4.
c) What can you conclude from the answers you have found in question a) and b).
Note: to solve this exercise you must print the graph. If you do not have a printer at home, you can transfer the parabola on a thin sheet of paper applying it on your screen and using a pen to copy the curve, the x and y-axis by transparency.
3.2 How many hours of daylight in Fairbanks, Alaska
The following graph shows the number of daylight hours during a day in Fairbanks (Alska) for each day of the year between the 1st of January and the 31st of December.
You can see on this graph, for instance, that the 1st of September there are only 5 hours of daylight in Fairbanks. And the 1st of January the hours of daylight are less than 1 hour. You are asked to answer the following questions by estimating the slope on the graph in hours/day. In order to simplify this math problem, you may consider that the calendar is made of 12 months of 30 days each.
a) On which day of the year the number of daylight hours increases the most between that day and the next one ? What is the maximum rate of change of daylight hours (in hours/day) ?
b) Find out the value of the derivative on the day found in a).
c) Do you think there are days of the year where the number of daylight hours is the same on that day and on the next one ? If it is the case, find out which are those days ? What is the value of the derivative of the curve on those days ?
d) On which date the rate of change in the number of daylight hours is
positive ? Is negative ? Deduce the sign of the derivative on those dates.
Note: to answer this math problem, you must print the graph. If you do not have a printer at home, you can transfer the parabola on a thin sheet of paper applying it on your screen and using a pen to copy the curve, the x and y-axis by transparency.
4. Derivatives applied to biology, medicine and economy
4.1 Decline of a bacteria population
A bactericide (or bacteriocide) has been introduced in the nutritive medium where a population of bacterias was growing. What happened then ? Well, the population kept growing but after a while it stopped and started to decline. The size of the population at time t is f(t) = 106 + 104 . t - 103 . t2.
f(t) is the number of bacterias and t is the time in hours.
You are asked to find the rate of growth, 
, at time t = 0 sec,
t = 5 hours and t = 10 hours.
4.2 Estimate a derivative graphically
Sketch a graph of the the derivative f '(x) for the function shown hereunder.
Note: to answer this math problem, you must print the graph. If you do not have a printer at home, you can transfer the parabola on a thin sheet of paper applying it on your screen and using a pen to copy the curve, the x and y-axis by transparency.
4.3 Demography of Drosophila (fly)
When a population is growing in a closed system you can observe that at the beginning its size is increasing slowly. This is because there are too few flies to procreate. After a while the population grows at a faster rate because the number of flies sexualy mature has increased sufficiently. However, resources become scarce rapidly, there is less room for each drosophila, less food, etc. Hence the growth of the population is slowing down and eventually it reaches the carrying capacity (the carrying capacity is the maximum population size that can be supported indefinitely by a given environment. The carrying capacity is achieved through a trade-off of birth and death rates).
This situation is described by a mathematical function which graph (shown hereunder) shows the growth of a drosophila population as a function of the time:
You are asked to:
a) Sketch the graph of the derivative of the hereabove curve. Which units are you going to use for the x and the y-axis ?
b) Find the days during which the population grows at the fastest and at the slowest rate.
Note: to answer this math problem, you must print the graph. If you do not have a printer at home, you can transfer the parabola on a thin sheet of paper applying it on your screen and using a pen to copy the curve, the x and y-axis by transparency.
4.4 Population of seals and polar bears in the Arctic Ocean Solution 4.4
The following graph shows the number of seals and polar bears in an arctic population. The growth of those two populations has been studied on a 600 day period.
Initial number of seals = 3000.
Initial number of polar bears = 400
Notice that the number of seals increases at the beginning because they reproduce very well. However, seals are being preyed on by polar bears. Therefore polar bears reproduce very well too because their food (the seals) is becoming more abundant. Then, while the number of polar bears is growing, the growth of the seal population is slowing down. Eventually the seal population declines. The following graph shows the derivative of the seal population with respect to time (this is the derivative of the blue curve hereabove).
Answer the following questions:
a) What is the value of the derivative of the seal population with respect to time when the number of seals is the highest ? The lowest ? Explain the meaning of the result obtained.
b) What is the size of the seal population when its derivative has a maximum value ? A minimum value ? Explain the meaning of the result obtained.
c) Which units must be used to express the slope of the first graph ? The vertical axis of the second graph ?
4.5 The diameter of your trachea is reduced by 33% of its original diameter when you are coughing Solution 4.5
When you are coughing, the airway (trachea) narrows to increase the speed of exhalation and to dislodge foreign bodies (see Bernouilli). This fact leads us to wonder: what is the required reduction in trachea diameter (in centimeters) during a cough to maximize the velocity of exhalation ? The following formula describes the relationship between v (velocity of exhalation in the trachea during a cough) and r (tracheal radius).
v = c . (r0 - r) . r2
v in cm/s,
c is a constant greater than zero. Its value depends on the lenght of the trachea,
r0 is the tracheal radius at rest ( = when you are not coughing),
r is the tracheal radius while coughing.
You are asked to:
a) Demonstrate that the velocity of the exhaled air, v, is maximum when r = (2/3).r0 , which means when the tracheal radius is reduced by 33,33% compared to its normal size at rest. The most remarkable thing is that the pictures taken with an X-ray device confirms the reduction of 33,33% calculated numerically.
b) Sketch the graph of v(r) and its derivative v'(r) using our free graph plotter online. Use the following values for r0 and c : r0 = 2 cm and c = 1. Do not forget to replace the variable r by the letter x in the equation you will enter in the graph plotter. Next, check graphically that the value of the radius r corresponding to the maximum exhaled velocity is two thirds of the value r0. Check graphically as well the value of the derivative, v'(r), when the exhaled velocity is maximum (the value of the derivative must be zero).
4.6 Cost and revenue in economics : maximize your profit (marginal cost, marginal revenue) Solution 4.6
In mathematical economics there is a relationship between revenue, r(x), and profit, p(x). The revenue is the money you get when you have produced (and thus sold) x items. The profit is calculated by substracting the costs, c(x), from revenues.
|
r(x) = revenues resulting from the production (and thus sale) of x items. c(x) = costs resulting from the production of x items (workforce salaries, heating cost, costs of leasing your office space,...) p(x) = r(x) – c(x) = profit due to the production (and thus sale) of x items. |
You can observe that the revenue, the cost and the profit are all functions of the number of items produced, x. Also the derivative of the revenue with respect to x, r'(x), gives the marginal revenue. However, we know that a derivative is the calculation of a slope. Hence the marginal revenue r'(x) represents a 
(for an infinitesimal interval of r and of x), which gives the slope of the curve at various levels of production, which means for different values of x. So we know, thanks to the marginal revenue, what will be the increase in revenue, 
, from producing (and thus selling) one more unit of a product (or one more item), 
.
The same goes for the derivative of the cost with respect to x, c'(x), which gives the marginal cost. The marginal cost is the increase in total cost as a result of producing one extra unit of product (or one extra item). The marginal cost is given for different production levels.
|
r'(x) = marginal revenue. c'(x) = marginal cost. |
You will find a graph hereunder that illustrates the important following fact:
|
The positive (= gain) maximum profit occurs at a production level (thus at a specific x value) where the marginal revenue is equal to the marginal cost : p(x) = max if r'(x) = c'(x) and p(x) > 0 |
Note: in economics, the break-even point is the point at which there is no net loss or gain, thus cost and revenue are equal : c(x) = r(x).
Look at the graph hereabove: if a company produces more than 3,6 items per year, it is working above the break-even point and thus the profit is positive. It is a net gain for the company. A positive profit occurs when the revenue curve is above the cost curve thus
p(x) = r(x) – c(x) > 0. The company is earning money (net gain).
In our example (check on the graph), the positive maximum profit occurs at a production level greater than the break-even point, when both green tangent lines are parallel.
This means that the maximum profit occurs when p'(x) = c'(x) – r'(x) = 0 (we find the x coordinate of the extrema using the first derivative of profit and looking for the value of x that gives a result that is equal to zero) thus when c'(x) = r'(x).
However, notice that at the far right of the graph the costs are greater than the revenues, this means that the company is loosing money. This might happen when a team is working inefficiently : in fact if the rate of production goes too high, operators must work overtime, machine maintenance cannot keep up, breakdowns occur, and the costs of production rise. Moreover, if this combines with a saturated market on which you cannot sell your product, the profit will sink.
To the left of the break-even point, the company is also loosing money. Costs are greater then revenues, the production is insufficient and revenues due to sales do not offset the high costs of production. The company is in a bad situation where
p'(x) = 0; c'(x) = r'(x) but p(x) is minimun and < 0. This is a situation where the profit is minimum and negative, thus the company is experiencing a maximum loss !
|
The maximum loss occurs for a level of production x where the green tangent lines are parallel too. However, in this case the situation is different from the maximum profit situation because here the cost curve is above the revenue curve : c(x) > r(x) thus |
You are asked to :
Given the following mathematical equations
r(x) = 10 . x
c(x) = x3 - 6.x2 + 15.x + 5
x = number of items produced, in thousands of units.
a) Is there a level of production for which the profit is maximum ? If your answer is yes, how many items must be sold to reach that level ?
b) Find a level of production to minimize the mean costs of production.
c) The level of production that maximize the profit is different or equal to the level that minimize the mean costs of production ?
d) After you have answered the questions a), b) and c), use the free graph plotter online to trace r(x), c(x) and their respective derivative to check your answers and visualize graphically what is hiding behind those mathematical functions and mysterious derivatives.