Derivatives - math : Answer of exercise 2
Basic math level

Find out graphically the slope of the tangent line to the parabola at x = -2 knowing that the parabola equation is y = x² + 1. Find out the derivative y' and the equation of the tangent line

a) Calculation of the derivative y ' of the quadratic equation (parabola equation)

y ' = (x² + 1) ' = 2x

b) Calculate graphically the slope of the tangent line to the parabola at x = -2

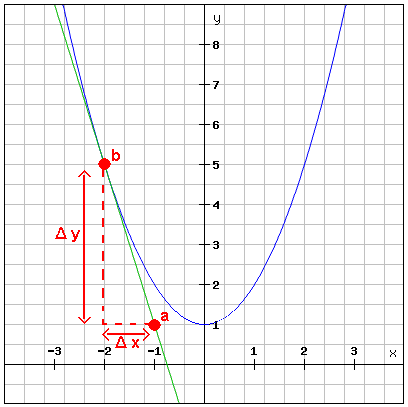
Slope of the tangent line =

c) Find the equation of that tangent line

The general equation of a straight line is y = ax + b, where the coefficient a is the slope of the line.

Given that the slope of our tangent line is –4,

thus the equation of the tangent line will be
y = -4x + b.

What is the value of the b term ?

Knowing that the tangent line is tangent to the parabola at x = -2, thus at y = (-2)² + 1 = 5, we can now figure out the b term (y-intercept) of the line that has a slope a = -4 and that passes through the point (-2 ; 5) :

        Tangent line equation : y = -4x + b,

        we know that (x ; y) = (-2 ; 5) satisfies this equation.

        Thus 5 = -4(-2) + b,

        and 5 + 4(-2) = b,

        which eventually yields b = 5 - 8 = -3.

        Conclusion : the tangent line equation is y = - 4x - 3

d) Calculate the derivative of the tangent

y ' = (-4x - 3) ' = - 4

e) Reach a conclusion on the results obtained in b) and d)

The derivative of the tangent line equation, computed in d), is equal to the slope of that tangent line, computed in b).

Calculate a derivative is the same than calculate a slope and inversely.

It is also interesting to notice that the derivative of the parabola is f '(x) = (x² + 1) ' = 2x.

f '(x) = 2x is the equation of the derivative of the parabola but it is also the equation of the slopes of the tangent lines to the parabola at various points on the curve.

In other words, f '(x) = 2x expresses the slope of the curve for various value of x.

For instance, what is the value of the slope of the parabola at x = -2 ?

f '(-2) = 2(-2) = -4.

Or, for instance, what is the slope of the curve at x = 1 ?

f '(1) = 2(1) = 2.