Derivative : solution exercise 2 (Intermediate math level)

Given the function , you are asked to:

a) Figure out the derivative f '(x) of this function

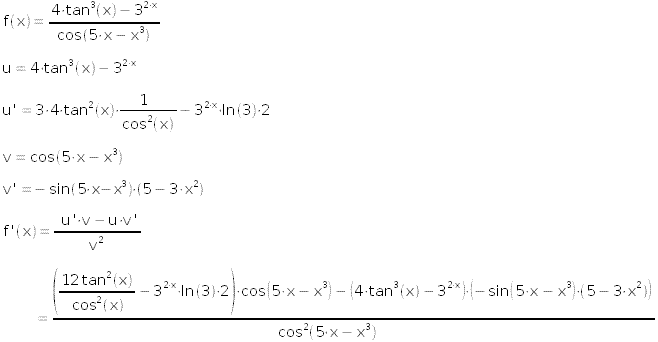
b) Find out the cartesian equation of the tangent line to f(x) at x = 0

General cartesian equation of a straight line : y = ax + b where a = f '(0)



f '(0) = -2 is the slope a of the tangent line to the curve at x = 0.
Thus the equation of that tangent line is : y = -2 ln(3) x + b, I know that it passes through the point that has an x-coordinate = 0 and an
y-coordinate = f(0) = (4 tan³(0) - 3⁰) / cos(0) = -1 / 1 = -1.
Then the equation of the tangent line that passes through the point (0 ; -1) is :

      y = -2 ln(3) x + b

      -1 = -2 ln(3) 0 + b

      Which yields b = -1.

      Conclusion: the tangent line is determined by the following equation y = -2 ln(3) x - 1

Here is the graph of the curve and its tangent line, traced thanks to the free Graph Plotter online (uncheck the box "Errors" to avoid the display of an annoying error message).